Una nueva técnica matemática muestra cómo construir pequeños objetos en cualquier dimensión que giran como una rueda, ampliando nuestra comprensión del espacio de dimensiones superiores.
Por Max Springer
Los matemáticos están “reinventando la rueda” dándole una nueva forma. La rueda que han imaginado parece una púa de guitarra multidimensional y, en teoría, podría girar de maneras que escapan a nuestra comprensión tridimensional. Este avance resuelve un problema de geometría que data de hace décadas al mostrar cómo construir objetos en dimensiones que no podemos imaginar.
“Es una teoría sorprendente”, afirma Gil Kalai, profesor del Instituto Einstein de Matemáticas en Israel, que no participó en el estudio. Los resultados demuestran que estos objetos insondables pueden construirse en cualquier dimensión y con una fracción del tamaño de las formas rodantes más tradicionales, como círculos o esferas.
Las ruedas giran porque son objetos con un “ancho constante”: parecen tener el mismo ancho desde cualquier ángulo. Esta propiedad geométrica permite que las ruedas mantengan una distancia constante entre dos planos paralelos, como el suelo y un automóvil, mientras se mueven. Básicamente, una forma tiene un ancho constante si puede rodar suavemente sin tambalearse. Por ejemplo, coloca una pelota de tenis entre tus manos paralelas y gírala: verás que tus manos nunca se acercan ni se alejan porque la pelota tiene una geometría de ancho constante. Una forma oblonga como un huevo no pasaría esa prueba.
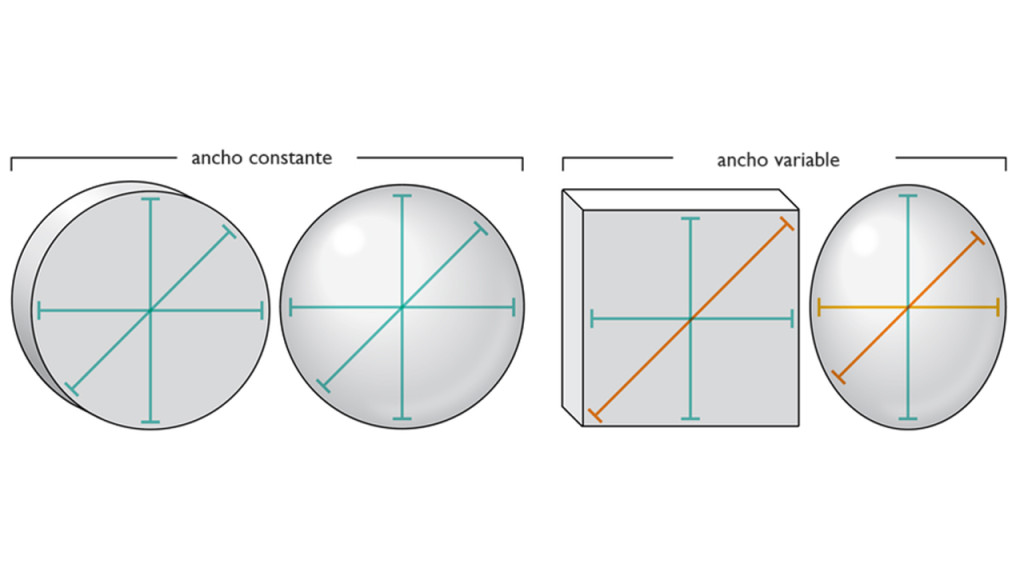
Los círculos y las esferas son ejemplos simples e intuitivos de formas de ancho constante, y los humanos las han estado utilizando para facilitar el movimiento durante milenios. Se trata de tipos especiales de formas de ancho constante llamadas “bolas”, formas en las que todos los puntos límite están a la misma distancia del centro. Se trata de un círculo en dos dimensiones y una esfera en tres, y el concepto se extiende a dimensiones superiores que no podemos visualizar fácilmente.
Como los puntos límite están todos situados a una distancia fija de un punto central, estas bolas son pesadas: tienen el máximo volumen posible para una forma de ancho constante en cualquier dimensión. Pero ser tan voluminosas no siempre es ideal. En la década de 1980, el matemático Oded Schramm planteó la pregunta: ¿cómo podemos encontrar formas de ancho constante con el mínimo volumen en cualquier dimensión? Esa “es una pregunta muy básica”, explica Kalai, una que los matemáticos han estado interesados en resolver desde entonces. «Pero nadie tenía ningún método para investigarla».
El problema se mantuvo hasta junio de este año, cuando un equipo internacional de matemáticos propuso una nueva forma de construir formas de ancho constante . El método de los investigadores, que implica la intersección de un número infinito de bolas n -dimensionales, se publicó en el servidor de preimpresión arXiv.org en una prueba concisa de tres páginas . “La receta en sí es muy simple”, dice el coautor del estudio Andriy Bondarenko, profesor de matemáticas en la Universidad Noruega de Ciencia y Tecnología. Aunque usar y analizar esta receta es relativamente sencillo, los investigadores tardaron años en “[entender] por qué deberíamos considerar esta receta en primer lugar”.
Ruedas en Flatland
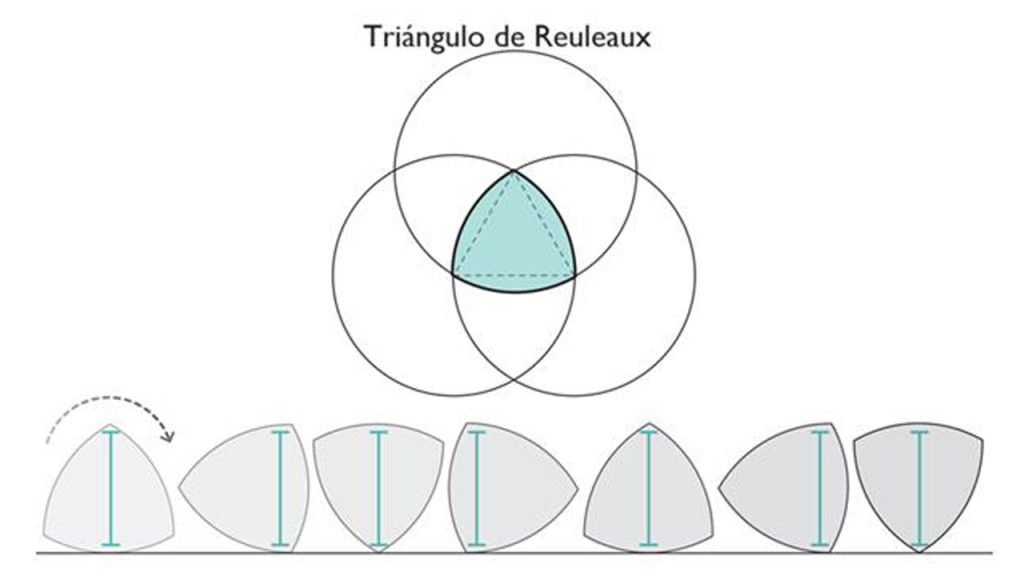
Este último trabajo es pionero en la investigación de formas de ancho constante en cualquier dimensión, pero diseñar ruedas en dos o tres dimensiones no es en sí un problema nuevo. Para estas dimensiones inferiores, que son fáciles de entender, los matemáticos han descubierto muchas formas de ancho constante con volúmenes más pequeños. En dos dimensiones, el triángulo de Reuleaux tiene el área más pequeña de las formas de ancho constante. Puedes dibujar esta forma tú mismo utilizando una especie de diagrama de Venn de tres vías. Primero, dibuja un triángulo equilátero, luego agrega tres círculos de igual radio alrededor de cada esquina. En el centro de estos círculos, encontrarás una forma redondeada que rueda como un círculo con solo una fracción del tamaño.
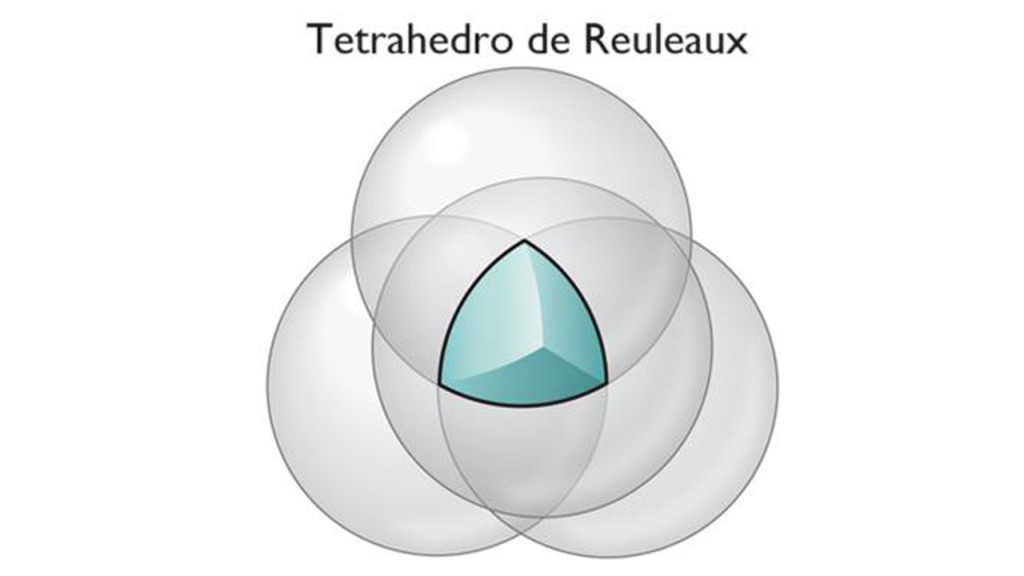
En tres dimensiones, se puede utilizar un método similar: se parte de un tetraedro regular, una figura formada por cuatro triángulos equiláteros, y se añade una esfera a cada uno de sus vértices. La figura resultante en el centro de estas esferas superpuestas se conoce como tetraedro de Reuleaux. No es exactamente de ancho constante; se acerca, pero los bordes sobresalen demasiado. Sin embargo, con un poco de lijado se obtiene una figura de ancho constante. Esto se puede hacer de dos maneras diferentes para formar dos figuras ligeramente diferentes llamadas cuerpos de Meissner.
Pero las sencillas fórmulas que se esconden detrás de estas formas no ofrecen ninguna pista sobre cómo construir en cuatro o más dimensiones, algo que escapa a la percepción humana. “Es increíblemente difícil generalizar la construcción de Reuleaux”, afirma Bondarenko. “Si fuera fácil, alguien lo habría hecho antes”.
Ruedas de dimensiones superiores
El último trabajo proporciona un algoritmo general para construir objetos de ancho constante en cualquier dimensión mediante la extensión del método de intersección de Reuleaux. El equipo de matemáticos utilizó un enfoque similar a un diagrama de Venn para obtener la nueva forma: una pieza geométricamente anómala en el centro de un espacio de dimensiones superiores.
Para representar esto en dos dimensiones, dibuja de nuevo un triángulo equilátero, seguido de un círculo centrado alrededor de uno de los vértices del triángulo, con un radio tan largo como cada uno de los catetos del triángulo. Luego imagina mover ese círculo de modo que su punto central siga el contorno del triángulo, subiendo por cada cateto y pasando cada vértice antes de regresar al punto de partida. A medida que el círculo se mueve, hay algunos lugares que ocupa constantemente. Esta intersección de las infinitas posiciones del círculo en movimiento forma una forma familiar: la rueda de Reuleaux, una generalización del triángulo de Reuleaux. “Al hacer esto, tienes esencialmente la misma construcción que con el triángulo de Reuleaux, excepto que aquí tomamos la intersección de infinitas bolas en lugar de solo tres o cuatro”, explica Andrii Arman, matemático de la Universidad de Manitoba y coautor del estudio.
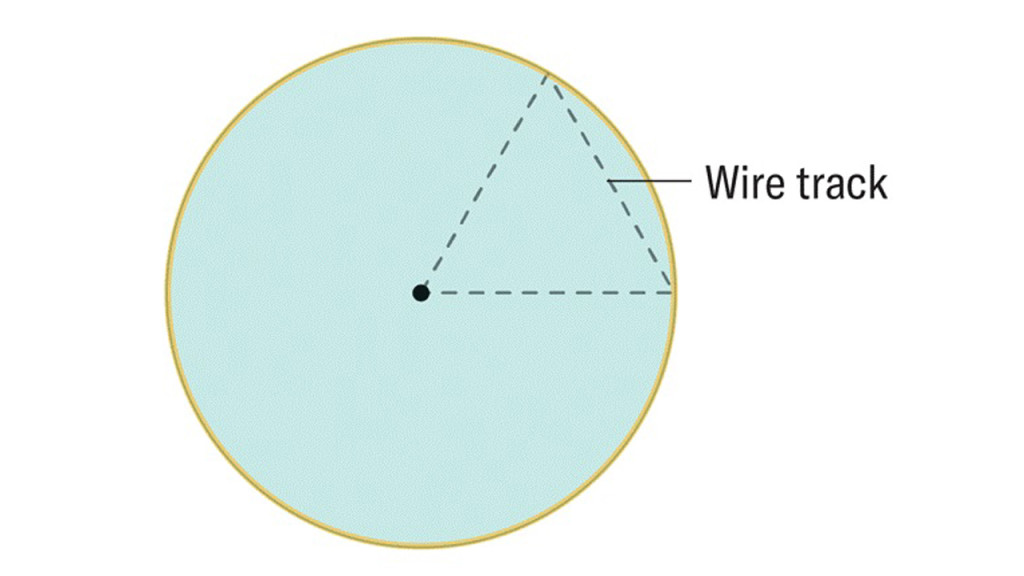
Esta técnica simple y computable puede revelar un objeto de ancho constante en cualquier dimensión, siempre que el límite alrededor del cual arrastramos nuestro círculo se seleccione correctamente para cada dimensión. Según la nueva investigación, seleccionar este límite en cualquier dimensión se reduce a una receta básica. En dos dimensiones, trazamos el círculo alrededor de un cuarto de círculo más pequeño en lugar de un triángulo equilátero. En tres, lo estrechamos aún más de un cuarto a un octavo de una esfera, y este patrón se extiende a dimensiones superiores mediante el aumento de potencias de 2. Al crear un límite de este tipo en n dimensiones y mover una bola n -dimensional correspondiente a lo largo de él, se traza un diagrama de Venn de dimensiones superiores, cuyo centro, según demuestran los autores, siempre debe tener un ancho de exactamente 2, lo que da lugar a su nueva forma en cualquier dimensión.
Este enfoque infinito, en lugar de finito, para construir formas no solo garantiza un ancho constante, sino que también hace que calcular su volumen en un espacio de dimensiones superiores sea sencillo. En comparación, las construcciones anteriores implican la estimación de una integral sobre muchas variables, mientras que el trabajo más reciente implica solo dos variables independientemente de la dimensión de la forma. “Es realmente difícil estimar el volumen en dimensiones altas”, dice Kalai, pero “toda esta [prueba] es bastante simple y muy elegante”.
El volumen del nuevo objeto es 0,9n veces menor que el de una pelota de n dimensiones, lo que significa que el volumen disminuye exponencialmente con cada dimensión adicional. Si bien las formas disminuyen de tamaño a un ritmo creciente al pasar a un espacio de dimensiones superiores, no son los objetos más pequeños posibles que mantienen un ancho constante. “Se supone que los cuerpos de Meissner poseen el menor volumen posible” en tres dimensiones, dice Bondarenko, y agrega: “Nuestro resultado es solo un 0,14 por ciento mayor que eso”.
Kalai sugiere que la creación de estas formas en dimensiones superiores con una serie infinita “puede ser el comienzo de una nueva era en el estudio de conjuntos con ancho constante”. Ahora que el problema original se ha verificado, “estamos en territorio desconocido”, concluye, pero armados con estos nuevos métodos, “hay alguna esperanza de abordar muchos problemas nuevos”.
(*) Max Springer es candidato a doctorado en Matemáticas Aplicadas en la Universidad de Maryland y becario AAAS Mass Media 2024 en Scientific American .
Fuente: Revista Nature




